科研-0005-多源融合导航学习

多源融合导航

1. 惯性导航

1.1 前言

惯性导航部分知识重新学习，学习材料使用武汉大学牛小骥老师的《惯性导航算法》课程课件。

1.2 惯导机械编排算法

1.2.0 预备知识

符号说明：

$$位置:\boldsymbol{r}_{Rb}^{p} \\ 速度:\boldsymbol{v}_{Rb}^{p} \\ 角速度:\boldsymbol{w}_{Rb}^{p}$$

• $b$:载体坐标系

• $R$:参考坐标系

• $p$:投影坐标系

速度向量:

由位置向量$dr_{eb}$对时间求导获得

$$\boldsymbol{v}_{eb}= \frac{d\boldsymbol{r}_{eb}}{dt} \bigg|_{e}$$

角速度向量:

角速度向量常用转换

• 角速度向量取反

  $$\boldsymbol{\omega}_{Rb}^{p}=- \boldsymbol{\omega}_{bR}^{p}$$

• 角速度向量相加

  $$\boldsymbol{\omega}_{in}^{n}= \boldsymbol{\omega}_{ie}^{n}+ \boldsymbol{\omega}_{en}^{n}$$

向量坐标转换:

$$\boldsymbol{v}^{R}=\boldsymbol{C}_{b}^{R}\boldsymbol{v}^{b}$$

• 由$b$坐标系转换为$R$坐标系

向量积，反对称矩阵:

$$\boldsymbol{v} \times \boldsymbol{v}_{1}= \left| \begin{matrix} \boldsymbol{i}&\boldsymbol{j}&\boldsymbol{k} \\ v_{x}&v_{y}&v_{z} \\ v_{1x}&v_{1y}&v_{1z} \end{matrix} \right|= \left( \boldsymbol{v} \times \right) \boldsymbol{v}_{1}= \left[ \begin{matrix} 0&-v_{z}&v_{y} \\ v_{z}&0&-v_{x} \\ -v_{y}&v_{x}&0 \end{matrix} \right] \left[ \begin{matrix} v_{1x} \\ v_{1y} \\ v_{1z} \end{matrix} \right]$$

反对称矩阵的幂:

$$\left( \boldsymbol{v} \times \right)^{n}= \left \{ \begin{matrix} \left(-1 \right)^{ \left( n-1 \right)/2} \left| \boldsymbol{v} \right|^{n-1} \left( \boldsymbol{v} \times \right),n=1,3,5, \cdots \\ \left(-1 \right)^{ \left( n-2 \right)/2} \left| \boldsymbol{v} \right|^{n-2} \left( \boldsymbol{v} \times \right)^{2},n=2,4,6, \cdots \end{matrix} \right.$$

反对称矩阵的矩阵指数函数:

$$e^{ \left( \boldsymbol{v} \times \right)}=I_{3 \times 3}+ \frac{ \sin \left| \boldsymbol{v} \right|}{|\boldsymbol{v}|} \left( \boldsymbol{v} \times \right)+ \frac{1- \cos \left| \boldsymbol{v} \right|}{|\boldsymbol{v}|^{2}} \left( \boldsymbol{v} \times \right)^{2}$$

投影变换:

$$\left( \boldsymbol{v}^{R} \times \right)=\boldsymbol{C}_{b}^{R} \left( \boldsymbol{v}^{b} \times \right) \left( \boldsymbol{C}_{b}^{R} \right)^{T}$$

1.2.1 姿态算法

捷联惯导利用陀螺的原始测量值计算载体姿态矩阵，通过姿态矩阵把加速度计测量的载体的沿载体坐标系轴向的比力信息转换到特定的坐标系中（ 如导航坐标系然后进行导航解算。

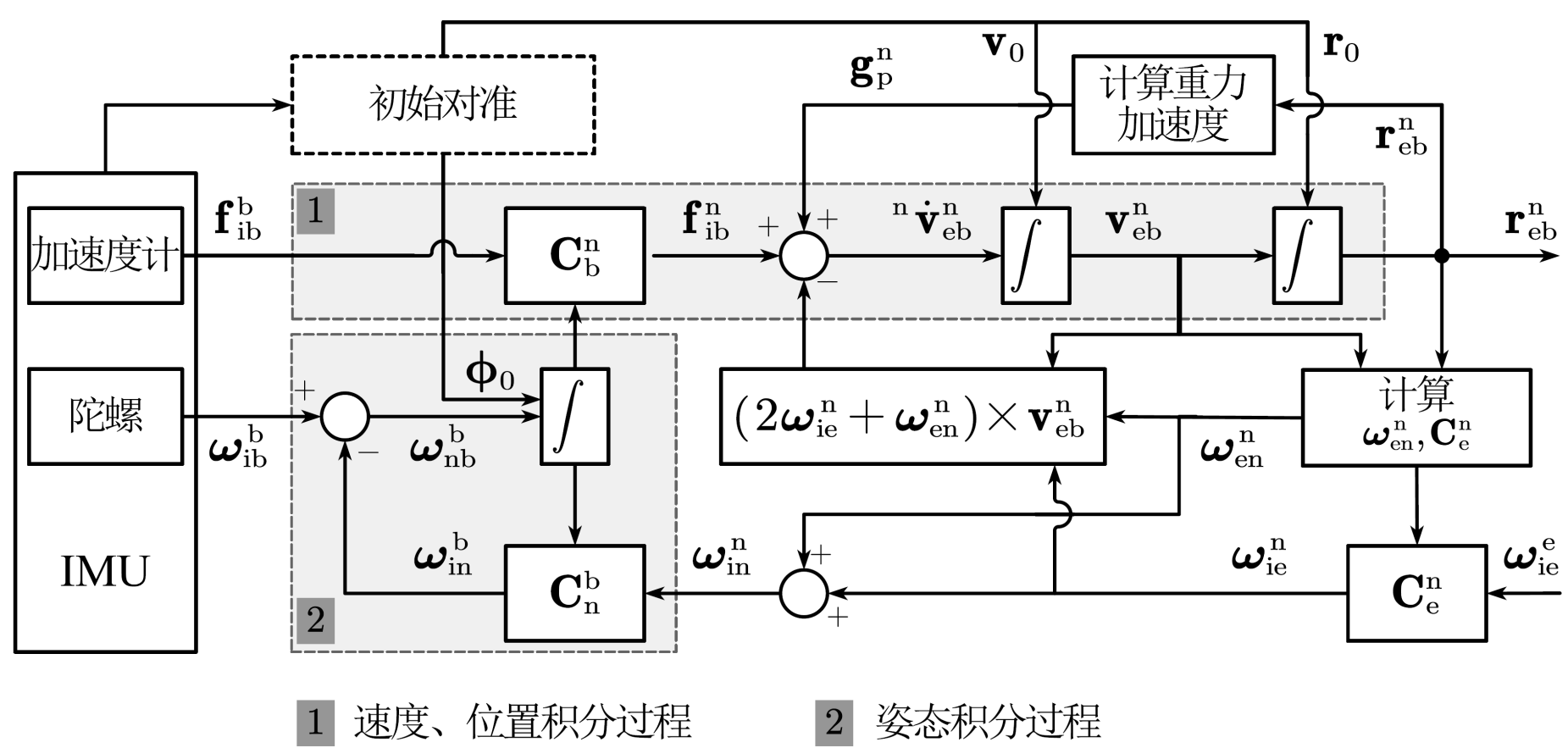
姿态(attitude)的定义

姿态（ attitude ）用于描述一个坐标系相对于另一个坐标系（参考坐标系）之间的角度关系，描述姿态需要
三个独立参数

1.2.1.1 欧拉角方法

欧拉角组

在三维欧氏空间里，任何两个正交坐标系都可以用坐标变换把它们联系起来，而坐标变换又可以用坐标系旋转 来得到。

一个动坐标系相对参考坐标系的方位，可以完全由动坐标系依次绕三个不同的转轴的转角来确定。

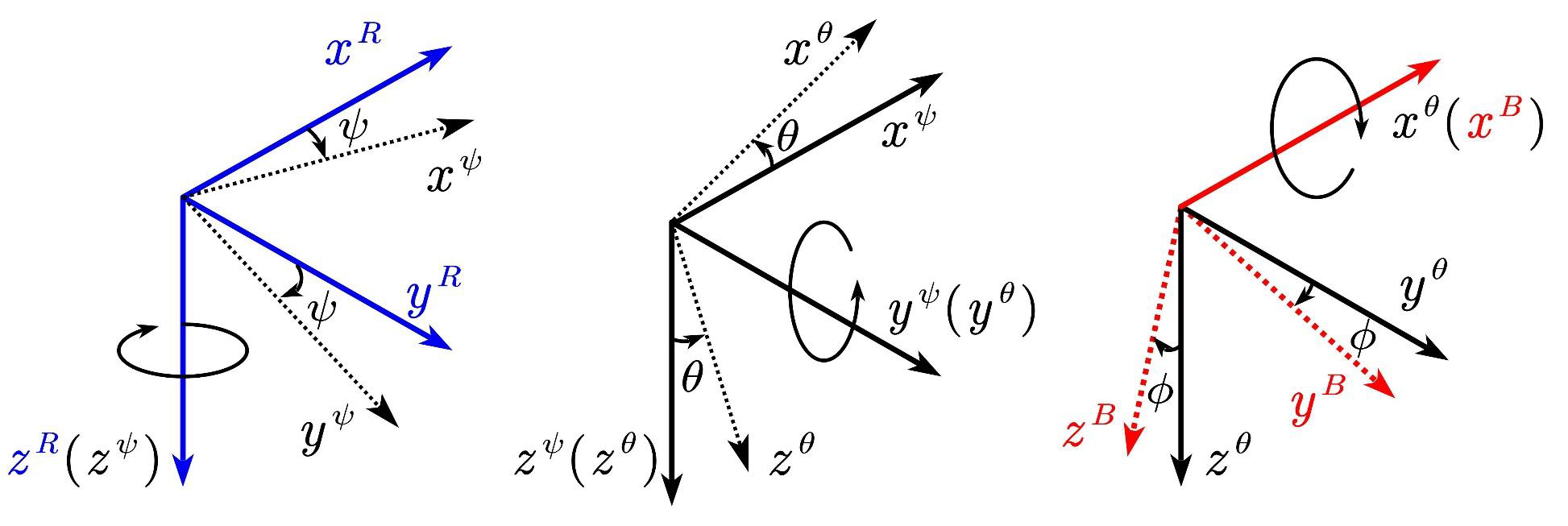
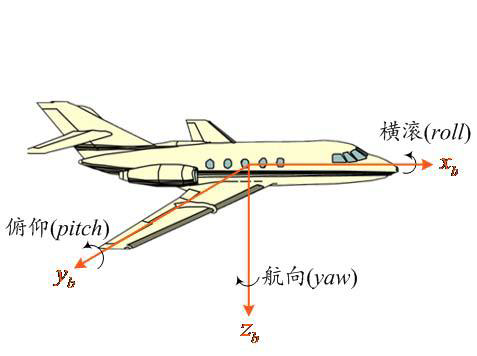
载具常用欧拉角组：航向角(yaw)$\psi$、俯仰角(pitch)$\theta$、横滚角(roll)$\phi$

• 航向角(yaw)$\psi$​：载体纵轴正方向在当地水平面上的投影与当地地理北向的夹角，取北偏东为正；取值范围*-180~180或0~360*
• 俯仰角(pitch)$\theta$​：载体纵轴正方向与其水平投影线之间的夹角，当载体“抬头”时定义为正，取值范围为*-90~90*
• 横滚角(roll)$\phi$：载体立轴正方向与载体纵轴所在铅垂面之间的夹角，当载体向右倾斜（如飞机右机翼下压）时为正，取值范围为*-180~180*

基于欧拉角的坐标转换表达式

坐标向量从$n$坐标系转换为$b$坐标系的表达式为：

$$\boldsymbol{r}^{b}=\boldsymbol{C}_{ \phi}\boldsymbol{C}_{ \theta}\boldsymbol{C}_{ \psi}r^{n}$$

也可写作为：

$$\boldsymbol{C}_{n}^{b}= \boldsymbol{C}_{ \phi} \boldsymbol{C}_{ \theta} \boldsymbol{C}_{ \psi}= \left[ \begin{matrix} c \theta c \psi&c \theta s \psi&-s \theta \\ -c \phi s \psi+s \phi s \theta c \psi&c \phi c \psi+s \phi s \theta s \psi&s \phi c \theta \\ s \phi s \psi+c \phi s \theta c \psi&-s \phi c \psi+c \phi s \theta s \psi&c \phi c \theta \end{matrix} \right]$$

其中，$s=sin$，$c=cos$

欧拉角的微分方程

微分方程数学表达式为：

$$\left[ \begin{matrix} \dot{ \phi} \\ \dot{ \theta} \\ \dot{ \psi} \end{matrix} \right]= \left[ \begin{matrix} 1& \sin \phi \tan \theta& \cos \phi \tan \theta \\ 0& \cos \phi&- \sin \phi \\ 0& \frac{ \sin \phi}{ \cos \theta}& \frac{ \cos \phi}{ \cos \theta} \end{matrix} \right] \left[ \begin{matrix} \omega_{nb,x}^{b} \\ \omega_{nb,y}^{b} \\ \omega_{nb,z}^{b} \end{matrix} \right]$$

1.2.1.2 方向余弦矩阵方法

从$b$坐标系转换到$R$坐标系的方向余弦矩阵为：

$$\boldsymbol{v}^{R}= \left[ \begin{matrix} x^{ \prime} \\ y^{ \prime} \\ z^{ \prime} \end{matrix} \right]= \left[ \begin{matrix} I^{T}i&I^{T}j&I^{T}k \\ J^{T}i&J^{T}j&J^{T}k \\ K^{T}i&K^{T}j&K^{T}k \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ z \end{matrix} \right]=\boldsymbol{C}_{b}^{R} \boldsymbol{v}^{b}$$

其中，

• $i,j,k$为$b$坐标系中$x,y,z$轴的单位向量；
• $I,J,K$为$b$坐标系中$x,y,z$轴的单位向量；

1.2.2 速度算法

1.2.3 位置算法